Read Hex Values From a File in C

Base 16 numerical system

In mathematics and computing, the hexadecimal (too base xvi or simply hex) numeral arrangement is a positional numeral organization that represents numbers using a radix (base) of xvi. Unlike the decimal system representing numbers using 10 symbols, hexadecimal uses 16 distinct symbols, near frequently the symbols "0"–"9" to stand for values 0 to 9, and "A"–"F" (or alternatively "a"–"f") to represent values from 10 to xv.

Software developers and system designers widely use hexadecimal numbers because they provide a homo-friendly representation of binary-coded values. Each hexadecimal digit represents four bits (binary digits), besides known as a nibble (or nybble). For example, an 8-scrap byte tin take values ranging from 00000000 to 11111111 in binary form, which can be conveniently represented as 00 to FF in hexadecimal.

In mathematics, a subscript is typically used to specify the base. For example, the decimal value 52,533 would be expressed in hexadecimal as CD35₁₆. In programming, a number of notations are used to denote hexadecimal numbers, usually involving a prefix. The prefix 0x is used in C which would announce this value as 0xCD35.

Hexadecimal is used in the transfer encoding Base16, in which each byte of the plaintext is broken into two 4-flake values and represented by two hexadecimal digits.

Representation [edit]

Written representation [edit]

In almost current employ cases the messages A–F or a–f represent the values x–15, while the numerals 0–ix are used to represent their usual values.

There is no universal convention to utilise lowercase or majuscule, and so each is prevalent or preferred in item environments by community standards or convention; even mixed instance is used. Seven-segment displays apply mixed-case AbCdEF to brand digits that can be distinguished from each other.

In that location is some standardization of using spaces (rather than commas or another punctuation mark) to split up hex values in a long list. For example in the following hex dump each 8-bit byte is a 2-digit hex number, with spaces between them, while the 32-bit offset at the start is an 8-digit hex number.

                        00000000            57            69            6b            69            70            65            64            69            61            2c            20            74            68            65            xx            66            00000010            72            65            65            twenty            65            6e            63            79            63            6c            6f            70            65            64            69            61            00000020            20            74            68            61            74            xx            61            6e            79            6f            6e            65            20            63            61            6e            00000030            20            65            64            69            74            0a

Distinguishing from decimal [edit]

In contexts where the base is not articulate, hexadecimal numbers can be ambiguous and dislocated with numbers expressed in other bases. There are several conventions for expressing values unambiguously. A numerical subscript (itself written in decimal) tin can requite the base explicitly: 159₁₀ is decimal 159; 159₁₆ is hexadecimal 159, which is equal to 345₁₀. Some authors adopt a text subscript, such as 159_decimal and 159_hex, or 159_d and 159_h.

Donald Knuth introduced the use of a particular typeface to represent a particular radix in his book The TeXbook.^[one] Hexadecimal representations are written at that place in a typewriter typeface: 5A3

In linear text systems, such as those used in near computer programming environments, a variety of methods have arisen:

Unix (and related) shells, AT&T assembly linguistic communication and likewise the C programming language (and its syntactic descendants such as C++, C#, Go, D, Coffee, JavaScript, Python and Windows PowerShell) use the prefix 0x for numeric constants represented in hex: 0x5A3. Character and cord constants may limited grapheme codes in hexadecimal with the prefix \x followed by two hex digits: '\x1B' represents the Esc control grapheme; "\x1B[0m\x1B[25;1H" is a string containing 11 characters with ii embedded Esc characters.^[ii] To output an integer as hexadecimal with the printf office family unit, the format conversion code %X or %x is used.
In URIs (including URLs), character codes are written equally hexadecimal pairs prefixed with %: http://world wide web.example.com/proper noun%20with%20spaces where %20 is the lawmaking for the space (blank) character, ASCII lawmaking point xx in hex, 32 in decimal.
In XML and XHTML, characters can be expressed as hexadecimal numeric graphic symbol references using the notation &#tencode;, for instance ’ represents the graphic symbol U+2019 (the right single quotation mark). If in that location is no x the number is decimal (thus ’ is the same graphic symbol).^[3]
In the Unicode standard, a character value is represented with U+ followed by the hex value, east.thou. U+20AC is the Euro sign (€).
Colour references in HTML, CSS and Ten Window tin be expressed with six hexadecimal digits (two each for the red, green and blue components, in that order) prefixed with #: white, for example, is represented equally #FFFFFF.^[4] CSS besides allows 3-hexdigit abbreviations with one hexdigit per component: #FA3 abbreviates #FFAA33 (a golden orange: ).
In MIME (email extensions) quoted-printable encoding, grapheme codes are written equally hexadecimal pairs prefixed with =: Espa=F1a is "España" (F1 is the code for ñ in the ISO/IEC 8859-ane character gear up).^[5])
In Intel-derived assembly languages and Modula-2,^{[half dozen]} hexadecimal is denoted with a suffixed H or h: FFh or 05A3H. Some implementations require a leading zip when the first hexadecimal digit character is not a decimal digit, so one would write 0FFh instead of FFh. Some other implementations (such as NASM) allow C-style numbers (0x42).
Other assembly languages (6502, Motorola), Pascal, Delphi, some versions of Bones (Commodore), GameMaker Language, Godot and Forth use $ as a prefix: $5A3.
Some assembly languages (Microchip) use the notation H'ABCD' (for ABCD_sixteen). Similarly, Fortran 95 uses Z'ABCD'.
Ada and VHDL enclose hexadecimal numerals in based "numeric quotes": xvi#5A3#. For bit vector constants VHDL uses the notation x"5A3".^[vii]
Verilog represents hexadecimal constants in the form 8'hFF, where viii is the number of bits in the value and FF is the hexadecimal constant.
The Smalltalk language uses the prefix 16r: 16r5A3
PostScript and the Bourne shell and its derivatives denote hex with prefix 16#: xvi#5A3. For PostScript, binary data (such as epitome pixels) can exist expressed as unprefixed consecutive hexadecimal pairs: AA213FD51B3801043FBC...
Common Lisp uses the prefixes #x and #16r. Setting the variables *read-base*^[viii] and *print-base*^[9] to 16 can as well be used to switch the reader and printer of a Common Lisp system to Hexadecimal number representation for reading and printing numbers. Thus Hexadecimal numbers can exist represented without the #10 or #16r prefix lawmaking, when the input or output base has been inverse to xvi.
MSX Basic,^[ten] QuickBASIC, FreeBASIC and Visual Bones prefix hexadecimal numbers with &H: &H5A3
BBC Bones and Locomotive Basic use & for hex.^[xi]
TI-89 and 92 serial uses a 0h prefix: 0h5A3
ALGOL 68 uses the prefix 16r to announce hexadecimal numbers: 16r5a3. Binary, quaternary (base-4) and octal numbers can be specified similarly.
The most common format for hexadecimal on IBM mainframes (zSeries) and midrange computers (IBM i) running the traditional OS's (zOS, zVSE, zVM, TPF, IBM i) is Ten'5A3', and is used in Assembler, PL/I, COBOL, JCL, scripts, commands and other places. This format was common on other (and now obsolete) IBM systems as well. Occasionally quotation marks were used instead of apostrophes.
Whatsoever IPv6 address can be written every bit eight groups of four hexadecimal digits (sometimes called hextets), where each group is separated by a colon (:). This, for example, is a valid IPv6 accost: 2001:0db8:85a3:0000:0000:8a2e:0370:7334 or abbreviated by removing zeros equally 2001:db8:85a3::8a2e:370:7334 (IPv4 addresses are usually written in decimal).
Globally unique identifiers are written every bit thirty-two hexadecimal digits, often in unequal hyphen-separated groupings, for instance 3F2504E0-4F89-41D3-9A0C-0305E82C3301.

Other symbols for x–15 and mostly different symbol sets [edit]

The use of the letters A through F to stand for the digits above 9 was not universal in the early history of computers.

During the 1950s, some installations, such equally Bendix-xiv favored using the digits 0 through 5 with an overline to denote the values 10–15 as 0, 1, ii, 3, 4 and v.
The SWAC (1950)^[12] and Bendix Grand-fifteen (1956)^[13] ^[12] computers used the lowercase letters u, 5, west, x, y and z for the values x to fifteen.
The ORDVAC and ILLIAC I (1952) computers (and some derived designs, e.thou. BRLESC) used the uppercase letters M, S, Northward, J, F and L for the values 10 to 15.^[14] ^[12]
The Librascope LGP-30 (1956) used the letters F, 1000, J, K, Q and Due west for the values 10 to 15.^[15] ^[12]
On the PERM (1956) computer, hexadecimal numbers were written every bit letters O for naught, A to N and P for 1 to xv. Many auto instructions had mnemonic hex-codes (A=add, M=multiply, L=load, F=fixed-point etc.); programs were written without teaching names.^[16]
The Honeywell Datamatic D-1000 (1957) used the lowercase letters b, c, d, eastward, f, and m whereas the Elbit 100 (1967) used the uppercase letters B, C, D, E, F and G for the values 10 to 15.^[12]
The Monrobot XI (1960) used the letters S, T, U, Five, Due west and X for the values 10 to xv.^[12]
The NEC parametron estimator NEAC 1103 (1960) used the letters D, Thousand, H, J, Grand (and perchance V) for values 10–15.^[17]
The Pacific Data Systems 1020 (1964) used the messages 50, C, A, S, M and D for the values x to 15.^[12]
New numeric symbols and names were introduced in the Bibi-binary notation by Boby Lapointe in 1968. This notation did not go very pop.

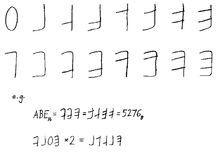
Bruce Alan Martin's hexadecimal notation proposal^[18]

Bruce Alan Martin of Brookhaven National Laboratory considered the choice of A–F "ridiculous". In a 1968 alphabetic character to the editor of the CACM, he proposed an entirely new set of symbols based on the bit locations, which did not gain much acceptance.^[18]
Some 7-segment display decoder fries (i.east., 74LS47) show unexpected output due to logic designed only to produce 0–9 correctly.^[19]

Verbal and digital representations [edit]

There are no traditional numerals to represent the quantities from ten to 15 – letters are used as a substitute – and nigh European languages lack non-decimal names for the numerals to a higher place 10. Even though English has names for several non-decimal powers (pair for the first binary ability, score for the outset vigesimal power, dozen, gross and great gross for the first three duodecimal powers), no English name describes the hexadecimal powers (decimal 16, 256, 4096, 65536, ... ). Some people read hexadecimal numbers digit past digit, like a phone number, or using the NATO phonetic alphabet, the Joint Army/Navy Phonetic Alphabet, or a similar ad-hoc organisation. In the wake of the adoption of hexadecimal amidst IBM System/360 programmers, Magnuson (1968)^[20] suggested a pronunciation guide that gave short names to the messages of hexadecimal – for case, "A" was pronounced "ann", B "bet", C "chris", etc.^[xx] Some other naming system was elaborated past Babb (2015), off a Tv set series equally a joke.^[21] Yet some other naming-organisation was published online by Rogers (2007)^[22] that tries to make the exact representation distinguishable in any case, even when the actual number does not contain numbers A–F. Examples are listed in the tables below.

Hexadecimal finger-counting scheme

Systems of counting on digits accept been devised for both binary and hexadecimal. Arthur C. Clarke suggested using each finger as an on/off bit, allowing finger counting from zero to 1023₁₀ on ten fingers.^[23] Some other organisation for counting upwards to FF₁₆ (255₁₀) is illustrated on the right.

Magnusson (1968)^[twenty]
naming method
Number	Pronunciation
A	ann
B	bet
C	chris
D	dot
East	ernest
F	frost
1A	annteen
A0	annty
5B	50-bet
A01C	annty christeen
1AD0	annteen dotty
3A7D	thirty-ann 70-dot

Rogers (2007)^[22]
naming method
Number	Pronunciation
A	ten
B	eleven
C	twelve
D	draze
E	eptwin
F	fim
ten	tex
eleven	oneteek
1F	fimteek
50	fiftek
C0	twelftek
100	hundrek
1000	thousek
3E	thirtek-eptwin
E1	eptek-i
C4A	twelve-hundrek-fourtek-ten
1743	ane-thousek-vii- -hundrek-fourtek-3

Signs [edit]

The hexadecimal arrangement tin can express negative numbers the same fashion as in decimal: −2A to represent −42₁₀ and and so on.

Hexadecimal tin can also be used to express the verbal chip patterns used in the processor, so a sequence of hexadecimal digits may represent a signed or even a floating-indicate value. This way, the negative number −42₁₀ can be written as FFFF FFD6 in a 32-bit CPU register (in two's-complement), as C228 0000 in a 32-bit FPU register or C045 0000 0000 0000 in a 64-bit FPU register (in the IEEE floating-point standard).

Hexadecimal exponential notation [edit]

Just every bit decimal numbers can exist represented in exponential note, so likewise tin hexadecimal numbers. By convention, the letter of the alphabet P (or p, for "ability") represents times two raised to the power of, whereas Eastward (or east) serves a similar purpose in decimal as part of the E annotation. The number later the P is decimal and represents the binary exponent. Increasing the exponent by 1 multiplies by 2, not xvi. 10.0p1 = 8.0p2 = iv.0p3 = 2.0p4 = 1.0p5. Usually, the number is normalized and then that the leading hexadecimal digit is 1 (unless the value is exactly 0).

Example: 1.3DEp42 represents $1.3DE 16 \times 2 42 x$ .

Hexadecimal exponential annotation is required past the IEEE 754-2008 binary floating-indicate standard. This notation can exist used for floating-signal literals in the C99 edition of the C programming language.^[24] Using the %a or %A conversion specifiers, this notation can be produced past implementations of the printf family of functions following the C99 specification^[25] and Single Unix Specification (IEEE Std 1003.1) POSIX standard.^[26]

Conversion [edit]

Binary conversion [edit]

Nigh computers manipulate binary information, but it is difficult for humans to work with a big number of digits for fifty-fifty a relatively modest binary number. Although most humans are familiar with the base 10 arrangement, information technology is much easier to map binary to hexadecimal than to decimal considering each hexadecimal digit maps to a whole number of bits (4₁₀). This instance converts 1111_two to base ten. Since each position in a binary numeral can comprise either a 1 or a 0, its value may be hands determined by its position from the correct:

0001_two = one_ten
0010₂ = two_x
0100₂ = iv₁₀
thou_two = eight_ten

Therefore:

1111₂	= eight₁₀ + 4₁₀ + ii₁₀ + 1₁₀
	= 15_ten

With footling practice, mapping 1111₂ to F₁₆ in 1 step becomes easy: encounter table in written representation. The reward of using hexadecimal rather than decimal increases rapidly with the size of the number. When the number becomes large, conversion to decimal is very tedious. Nevertheless, when mapping to hexadecimal, information technology is trivial to regard the binary string as iv-digit groups and map each to a single hexadecimal digit.^[27]

This example shows the conversion of a binary number to decimal, mapping each digit to the decimal value, and calculation the results.

(01011110101101010010)₂	= 262144₁₀ + 65536₁₀ + 32768₁₀ + 16384₁₀ + 8192₁₀ + 2048₁₀ + 512₁₀ + 256₁₀ + 64₁₀ + 16₁₀ + 2₁₀
	= 387922_ten

Compare this to the conversion to hexadecimal, where each group of four digits can be considered independently, and converted directly:

(01011110101101010010)₂	=	0101	1110	1011	0101	0010₂
	=	5	E	B	5	2_sixteen
	=	5EB52_sixteen

The conversion from hexadecimal to binary is equally direct.^[27]

Other uncomplicated conversions [edit]

Although 4th (base of operations 4) is little used, information technology tin easily be converted to and from hexadecimal or binary. Each hexadecimal digit corresponds to a pair of quaternary digits and each 4th digit corresponds to a pair of binary digits. In the above instance five Eastward B 5 2₁₆ = eleven 32 23 11 02₄.

The octal (base eight) system can also be converted with relative ease, although not quite every bit trivially as with bases 2 and 4. Each octal digit corresponds to three binary digits, rather than four. Therefore, we tin can convert between octal and hexadecimal via an intermediate conversion to binary followed by regrouping the binary digits in groups of either three or iv.

Partition-remainder in source base [edit]

Equally with all bases there is a simple algorithm for converting a representation of a number to hexadecimal past doing integer division and remainder operations in the source base of operations. In theory, this is possible from any base, but for most humans only decimal and for near computers merely binary (which can be converted by far more than efficient methods) tin be easily handled with this method.

Let d be the number to represent in hexadecimal, and the serial h_ih_i−i...h₂h₁ exist the hexadecimal digits representing the number.

i ← 1
h_i ← d modernistic 16
d ← (d − h_i) / 16
If d = 0 (render serial h_i) else increase i and go to stride ii

"16" may be replaced with any other base that may be desired.

The post-obit is a JavaScript implementation of the in a higher place algorithm for converting whatever number to a hexadecimal in String representation. Its purpose is to illustrate the above algorithm. To piece of work with data seriously, however, information technology is much more advisable to piece of work with bitwise operators.

                        office            toHex            (            d            )            {            var            r            =            d            %            16            ;            if            (            d            -            r            ==            0            )            {            return            toChar            (            r            );            }            return            toHex            ((            d            -            r            )            /            sixteen            )            +            toChar            (            r            );            }            office            toChar            (            north            )            {            const            alpha            =            "0123456789ABCDEF"            ;            render            alpha            .            charAt            (            n            );            }

Conversion through improver and multiplication [edit]

It is too possible to make the conversion past assigning each place in the source base the hexadecimal representation of its place value — before conveying out multiplication and addition to get the final representation. For case, to convert the number B3AD to decimal, one can split the hexadecimal number into its digits: B (11_x), 3 (3_ten), A (10₁₀) and D (13₁₀), and and then go the terminal result by multiplying each decimal representation by 16^p (p existence the corresponding hex digit position, counting from right to left, commencement with 0). In this case, we take that:

$B3AD = (eleven \times 16 3) + (iii \times xvi 2) + (10 \times 16 i) + (thirteen \times sixteen 0)$

which is 45997 in base ten.

Tools for conversion [edit]

Many computer systems provide a calculator utility capable of performing conversions between the various radices frequently including hexadecimal.

In Microsoft Windows, the Estimator utility can be set to Scientific mode (called Programmer mode in some versions), which allows conversions between radix 16 (hexadecimal), 10 (decimal), 8 (octal) and two (binary), the bases well-nigh ordinarily used by programmers. In Scientific Mode, the on-screen numeric keypad includes the hexadecimal digits A through F, which are agile when "Hex" is selected. In hex mode, however, the Windows Calculator supports only integers.

Elementary arithmetics [edit]

Unproblematic operations such addition, subtraction, multiplication and division can exist carried out indirectly through conversion to an alternating numeral system, such as the commonly-used decimal organization or the binary system where each hex digit corresponds to iv binary digits.

Alternatively, one tin can besides perform unproblematic operations directly inside the hex system itself — by relying on its addition/multiplication tables and its corresponding standard algorithms such as long division and the traditional subtraction algorithm.

Existent numbers [edit]

Rational numbers [edit]

As with other numeral systems, the hexadecimal system can be used to stand for rational numbers, although repeating expansions are common since sixteen (x₁₆) has only a single prime gene; two.

For any base, 0.ane (or "1/10") is always equivalent to one divided by the representation of that base value in its own number system. Thus, whether dividing 1 by 2 for binary or dividing one past sixteen for hexadecimal, both of these fractions are written as 0.1. Because the radix xvi is a perfect foursquare (4²), fractions expressed in hexadecimal accept an odd period much more than frequently than decimal ones, and at that place are no cyclic numbers (other than trivial single digits). Recurring digits are exhibited when the denominator in lowest terms has a prime gene not constitute in the radix; thus, when using hexadecimal annotation, all fractions with denominators that are non a power of ii result in an space string of recurring digits (such as thirds and fifths). This makes hexadecimal (and binary) less convenient than decimal for representing rational numbers since a larger proportion lie exterior its range of finite representation.

All rational numbers finitely representable in hexadecimal are likewise finitely representable in decimal, duodecimal and sexagesimal: that is, any hexadecimal number with a finite number of digits also has a finite number of digits when expressed in those other bases. Conversely, but a fraction of those finitely representable in the latter bases are finitely representable in hexadecimal. For example, decimal 0.1 corresponds to the infinite recurring representation 0.ane9 in hexadecimal. Still, hexadecimal is more efficient than duodecimal and sexagesimal for representing fractions with powers of 2 in the denominator. For example, 0.0625₁₀ (one-sixteenth) is equivalent to 0.1₁₆, 0.09₁₂, and 0;3,45₆₀.

due north	Decimal Prime factors of base, b = 10: 2, 5; b − 1 = 9: iii; b + 1 = 11: xi			Hexadecimal Prime number factors of base, b = sixteen₁₀ = 10: 2; b − 1 = 15₁₀ = F: iii, 5; b + 1 = 17₁₀ = eleven: 11
due north	Fraction	Prime factors	Positional representation	Positional representation	Prime factors	Fraction(1/n)
two	ane/two	ii	0.v	0.8	2	1/2
three	1/three	3	0.3333... = 0. 3	0.5555... = 0. 5	3	1/3
4	one/iv	2	0.25	0.four	2	1/4
v	1/v	v	0.2	0. iii	5	i/5
6	one/six	2 , 3	0.ane 6	0.2 A	2 , 3	one/six
vii	1/7	7	0. 142857	0. 249	7	1/7
eight	1/8	two	0.125	0.2	2	1/8
9	i/ix	iii	0. 1	0. 1C7	iii	1/ix
10	1/10	2 , five	0.one	0.1 ix	two , v	ane/A
eleven	1/11	xi	0. 09	0. 1745D	B	1/B
12	one/12	ii , 3	0.08 iii	0.1 v	2 , 3	1/C
xiii	1/13	13	0. 076923	0. 13B	D	1/D
14	1/14	2 , 7	0.0 714285	0.1 249	2 , seven	one/E
15	ane/15	3 , five	0.0 half dozen	0. i	3 , 5	one/F
16	1/16	2	0.0625	0.1	2	1/10
17	1/17	17	0. 0588235294117647	0. 0F	11	ane/eleven
18	one/18	2 , 3	0.0 5	0.0 E38	2 , 3	one/12
19	one/19	nineteen	0. 052631578947368421	0. 0D79435E5	13	1/xiii
20	one/20	2 , five	0.05	0.0 C	2 , v	1/14
21	1/21	3 , 7	0. 047619	0. 0C3	three , vii	i/15
22	1/22	ii , 11	0.0 45	0.0 BA2E8	2 , B	ane/16
23	1/23	23	0. 0434782608695652173913	0. 0B21642C859	17	1/17
24	1/24	2 , 3	0.041 six	0.0 A	2 , iii	1/xviii
25	1/25	5	0.04	0. 0A3D7	5	1/19
26	1/26	2 , 13	0.0 384615	0.0 9D8	2 , D	one/1A
27	1/27	3	0. 037	0. 097B425ED	3	ane/1B
28	1/28	ii , 7	0.03 571428	0.0 924	ii , 7	1/1C
29	i/29	29	0. 0344827586206896551724137931	0. 08D3DCB	1D	ane/1D
thirty	1/30	2 , iii , 5	0.0 three	0.0 8	two , 3 , five	1/1E
31	ane/31	31	0. 032258064516129	0. 08421	1F	1/1F
32	1/32	2	0.03125	0.08	ii	1/20
33	1/33	three , 11	0. 03	0. 07C1F	3 , B	1/21
34	one/34	2 , 17	0.0 2941176470588235	0.0 78	ii , xi	1/22
35	1/35	5 , vii	0.0 285714	0. 075	5 , seven	1/23
36	1/36	2 , 3	0.02 7	0.0 71C	two , three	1/24

Irrational numbers [edit]

The table beneath gives the expansions of some mutual irrational numbers in decimal and hexadecimal.

Number	Positional representation
Number	Decimal	Hexadecimal
√two (the length of the diagonal of a unit of measurement square)	ane.414213 562 373 095 048 ...	i.6A09E667F3BCD...
√3 (the length of the diagonal of a unit cube)	1.732050 807 568 877 293 ...	one.BB67AE8584CAA...
√v (the length of the diagonal of a i×two rectangle)	2.236067 977 499 789 696 ...	two.3C6EF372FE95...
$φ$ (phi, the gilt ratio = $(1+ \sqrt five)/ii$ )	ane.618033 988 749 894 848 ...	1.9E3779B97F4A...
$π$ (pi, the ratio of circumference to diameter of a circle)	iii.141592 653 589 793 238 462 643 383279 502 884 197 169 399 375 105 ...	three.243F6A8885A308D313198A2E0 3707344A4093822299F31D008...
$e$ (the base of the natural logarithm)	2.718281 828 459 045 235 ...	2.B7E151628AED2A6B...
$τ$ (the Thue–Morse abiding)	0.412454 033 640 107 597 ...	0.6996 9669 9669 6996...
$γ$ (the limiting deviation betwixt the harmonic series and the natural logarithm)	0.577215 664 901 532 860 ...	0.93C467E37DB0C7A4D1B...

Powers [edit]

Powers of ii have very simple expansions in hexadecimal. The first sixteen powers of 2 are shown below.

2^x	Value	Value (Decimal)
2⁰	one	i
2^one	ii	two
2²	iv	4
2³	viii	8
2⁴	10_hex	16_dec
ii⁵	20_hex	32_dec
2^{half dozen}	40_hex	64_dec
2^seven	eighty_hex	128_dec
2⁸	100_hex	256_december
two⁹	200_hex	512_dec
ii^A (two^10_dec)	400_hex	1024_dec
2^B (two^11_december)	800_hex	2048_dec
2^C (2^12_dec)	1000_hex	4096_december
2^D (2^13_dec)	2000_hex	8192_dec
2^{Due east} (2^fourteen_dec)	4000_hex	16,384_dec
two^F (2^15_dec)	8000_hex	32,768_dec
two¹⁰ (2^16_december)	10000_hex	65,536_dec

Cultural history [edit]

The traditional Chinese units of measurement were base of operations-16. For example, one jīn (斤) in the old system equals 16 taels. The suanpan (Chinese abacus) can be used to perform hexadecimal calculations such every bit additions and subtractions.^[28]

Equally with the duodecimal system, in that location have been occasional attempts to promote hexadecimal equally the preferred numeral system. These attempts ofttimes propose specific pronunciation and symbols for the individual numerals.^[29] Some proposals unify standard measures so that they are multiples of 16.^[thirty] ^[31] An early on such proposal was put forward by John West. Nystrom in Projection of a New Arrangement of Arithmetic, Weight, Measure and Coins: Proposed to be called the Tonal System, with Sixteen to the Base, published in 1862.^[32] Nystrom among other things suggested hexadecimal time, which subdivides a day past 16, so that there are 16 "hours" (or "10 tims", pronounced tontim) in a day.^[33]

Expect up hexadecimal in Wiktionary, the complimentary dictionary.

The word hexadecimal is get-go recorded in 1952.^[34] It is macaronic in the sense that it combines Greek ἕξ (hex) "six" with Latinate -decimal. The all-Latin alternative sexadecimal (compare the word sexagesimal for base 60) is older, and sees at least occasional use from the late 19th century.^[35] Information technology is still in use in the 1950s in Bendix documentation. Schwartzman (1994) argues that apply of sexadecimal may accept been avoided because of its suggestive abbreviation to sex.^[36] Many western languages since the 1960s have adopted terms equivalent in formation to hexadecimal (e.1000. French hexadécimal, Italian esadecimale, Romanaian hexazecimal, Serbian хексадецимални, etc.) but others accept introduced terms which substitute native words for "sixteen" (east.g. Greek δεκαεξαδικός, Icelandic sextándakerfi, Russian шестнадцатеричной etc.)

Terminology and note did not become settled until the terminate of the 1960s. Donald Knuth in 1969 argued that the etymologically right term would be senidenary, or possibly sedenary, a Latinate term intended to convey "grouped by 16" modelled on binary, ternary and fourth etc. According to Knuth'due south argument, the correct terms for decimal and octal arithmetic would exist denary and octonary, respectively.^[37] Alfred B. Taylor used senidenary in his mid-1800s piece of work on culling number bases, although he rejected base sixteen because of its "incommodious number of digits".^[38] ^[39]

The now-current annotation using the letters A to F establishes itself as the de facto standard beginning in 1966, in the wake of the publication of the Fortran IV transmission for IBM Organization/360, which (unlike earlier variants of Fortran) recognizes a standard for entering hexadecimal constants.^[twoscore] Equally noted above, alternative notations were used by NEC (1960) and The Pacific Data Systems 1020 (1964). The standard adopted by IBM seems to have become widely adopted past 1968, when Bruce Alan Martin in his letter to the editor of the CACM complains that

"With the ridiculous choice of letters A, B, C, D, E, F as hexadecimal number symbols adding to already troublesome bug of distinguishing octal (or hex) numbers from decimal numbers (or variable names), the time is overripe for reconsideration of our number symbols. This should have been done before poor choices gelled into a de facto standard!"

Martin'due south statement was that apply of numerals 0 to 9 in nondecimal numbers "imply to the states a base-ten place-value scheme": "Why not apply entirely new symbols (and names) for the vii or 15 nonzero digits needed in octal or hex. Fifty-fifty employ of the letters A through P would exist an improvement, only entirely new symbols could reflect the binary nature of the system".^[eighteen]

Base16 (transfer encoding) [edit]

Base16 (as a proper proper name without a infinite) can also refer to a binary to text encoding belonging to the same family equally Base32, Base58, and Base64.

In this case, data is broken into four-bit sequences, and each value (between 0 and 15 inclusively) is encoded using 16 symbols from the ASCII character set. Although whatsoever 16 symbols from the ASCII character ready can be used, in practice the ASCII digits '0'–'9' and the messages 'A'–'F' (or the lowercase 'a'–'f') are always called in order to marshal with standard written notation for hexadecimal numbers.

At that place are several advantages of Base16 encoding:

Most programming languages already have facilities to parse ASCII-encoded hexadecimal
Being exactly half a byte, 4-bits is easier to process than the v or half dozen bits of Base32 and Base64 respectively
The symbols 0–9 and A-F are universal in hexadecimal annotation, so it is easily understood at a glance without needing to rely on a symbol lookup table
Many CPU architectures have dedicated instructions that permit admission to a half-byte (otherwise known as a "nibble"), making it more efficient in hardware than Base32 and Base64

The main disadvantages of Base16 encoding are:

Space efficiency is just 50%, since each iv-chip value from the original data will be encoded equally an eight-bit byte. In contrast, Base32 and Base64 encodings accept a infinite efficiency of 63% and 75% respectively.
Possible added complexity of having to accept both capital and lowercase letters

Support for Base16 encoding is ubiquitous in modern computing. It is the basis for the W3C standard for URL percent encoding, where a character is replaced with a percent sign "%" and its Base16-encoded class. Most modern programming languages directly include support for formatting and parsing Base16-encoded numbers.

Come across also [edit]

Base32, Base64 (content encoding schemes)
Hexadecimal fourth dimension
IBM hexadecimal floating-bespeak
Hex editor
Hex dump
Bailey–Borwein–Plouffe formula (BBP)
Hexspeak

References [edit]

^ Donald E. Knuth. The TeXbook (Computers and Typesetting, Volume A). Reading, Massachusetts: Addison–Wesley, 1984. ISBN 0-201-13448-9. The source lawmaking of the book in TeX Archived 2007-09-27 at the Wayback Machine (and a required gear up of macros CTAN.org) is bachelor online on CTAN.
^ The string "\x1B[0m\x1B[25;1H" specifies the character sequence Esc [ 0 grand Esc [ 2 5 ; 1 H Nul. These are the escape sequences used on an ANSI terminal that reset the character set and color, and so motility the cursor to line 25.
^ "The Unicode Standard, Version vii" (PDF). Unicode. Archived (PDF) from the original on 2016-03-03. Retrieved 2018-ten-28 .
^ "Hexadecimal web colors explained". Archived from the original on 2006-04-22. Retrieved 2006-01-11 .
^ "ISO-8859-1 (ISO Latin 1) Character Encoding". www.ic.unicamp.br. Archived from the original on 2019-06-29. Retrieved 2019-06-26 .
^ "Modula-two – Vocabulary and representation". Modula −2. Archived from the original on 2015-12-13. Retrieved 2015-xi-01 .
^ "An Introduction to VHDL Data Types". FPGA Tutorial. 2020-05-10. Archived from the original on 2020-08-23. Retrieved 2020-08-21 .
^ "*read-base of operations* variable in Common Lisp". CLHS. Archived from the original on 2016-02-03. Retrieved 2015-01-10 .
^ "*print-base of operations* variable in Common Lisp". CLHS. Archived from the original on 2014-12-26. Retrieved 2015-01-10 .
^ MSX is Coming — Part 2: Inside MSX Archived 2010-11-24 at the Wayback Machine Compute!, outcome 56, January 1985, p. 52
^ BBC BASIC programs are not fully portable to Microsoft Basic (without modification) since the latter takes & to prefix octal values. (Microsoft BASIC primarily uses &O to prefix octal, and information technology uses &H to prefix hexadecimal, but the ampersand alone yields a default estimation as an octal prefix.
^ ^a ^b ^c ^d ^e ^f ^grand Savard, John J. K. (2018) [2005]. "Computer Arithmetics". quadibloc. The Early Days of Hexadecimal. Archived from the original on 2018-07-16. Retrieved 2018-07-xvi .
^ "2.1.three Sexadecimal notation". G15D Programmer'south Reference Manual (PDF). Los Angeles, CA, USA: Bendix Computer, Partition of Bendix Aviation Corporation. p. 4. Archived (PDF) from the original on 2017-06-01. Retrieved 2017-06-01 . This base of operations is used considering a group of four $.25 can represent any one of sixteen different numbers (zero to xv). Past assigning a symbol to each of these combinations nosotros get in at a notation called sexadecimal (usually hex in chat because nobody wants to abridge sex). The symbols in the sexadecimal linguistic communication are the ten decimal digits and, on the G-xv typewriter, the letters u, v, due west, x, y and z. These are arbitrary markings; other computers may apply different alphabet characters for these final six digits.
^ Gill, South.; Neagher, R. E.; Muller, D. East.; Nash, J. P.; Robertson, J. E.; Shapin, T.; Whesler, D. J. (1956-09-01). Nash, J. P. (ed.). "ILLIAC Programming – A Guide to the Preparation of Problems For Solution by the University of Illinois Digital Estimator" (PDF). bitsavers.org (Fourth printing. Revised and corrected ed.). Urbana, Illinois, United states of america: Digital Reckoner Laboratory, Graduate College, University of Illinois. pp. 3–2. Archived (PDF) from the original on 2017-05-31. Retrieved 2014-12-18 .
^ Regal PRECISION Electronic Computer LGP – 30 PROGRAMMING Transmission. Port Chester, New York: Royal McBee Corporation. April 1957. Archived from the original on 2017-05-31. Retrieved 2017-05-31 . (NB. This somewhat odd sequence was from the next vi sequential numeric keyboard codes in the LGP-thirty'south 6-bit character lawmaking.)
^ Manthey, Steffen; Leibrandt, Klaus (2002-07-02). "Die PERM und ALGOL" (PDF) (in German). Retrieved 2018-05-19 .
^ NEC Parametron Digital Computer Blazon NEAC-1103 (PDF). Tokyo, Japan: Japan Electric Company Ltd. 1960. True cat. No. 3405-C. Archived (PDF) from the original on 2017-05-31. Retrieved 2017-05-31 .
^ ^a ^b ^c Martin, Bruce Alan (October 1968). "Letters to the editor: On binary notation". Communications of the ACM. Associated Universities Inc. eleven (10): 658. doi:10.1145/364096.364107. S2CID 28248410.
^ "Archived re-create". Archived (PDF) from the original on 2021-10-20. Retrieved 2021-09-15 . {{cite web}}: CS1 maint: archived copy as championship (link)
^ ^a ^b ^c Magnuson, Robert A. (January 1968). "A hexadecimal pronunciation guide". Datamation. Vol. 14, no. ane. p. 45.
^ Babb, Tim (2015). "How to pronounce hexadecimal". Bzarg. Archived from the original on 2020-xi-eleven. Retrieved 2021-01-01 .
^ ^a ^b Rogers, Southward.R. (2007). "Hexadecimal number words". Intuitor. Archived from the original on 2019-09-17. Retrieved 2019-08-26 .
^ Clarke, Arthur; Pohl, Frederik (2008). The Concluding Theorem . Ballantine. p. 91. ISBN978-0007289981.
^ "ISO/IEC 9899:1999 – Programming languages – C". ISO. Iso.org. 2011-12-08. Archived from the original on 2016-ten-10. Retrieved 2014-04-08 .
^ "Rationale for International Standard – Programming Languages – C" (PDF). Open up Standards. 5.10. April 2003. pp. 52, 153–154, 159. Archived (PDF) from the original on 2016-06-06. Retrieved 2010-10-17 .
^ The IEEE and The Open Group (2013) [2001]. "dprintf, fprintf, printf, snprintf, sprintf – impress formatted output". The Open Group Base of operations Specifications (Issue vii, IEEE Std 1003.i, 2013 ed.). Archived from the original on 2016-06-21. Retrieved 2016-06-21 .
^ ^a ^b Mano, M. Morris; Ciletti, Michael D. (2013). Digital Pattern – With an Introduction to the Verilog HDL (Fifth ed.). Pearson Education. pp. half dozen, 8–ten. ISBN978-0-13-277420-8.
^ "算盤 Hexadecimal Addition & Subtraction on an Chinese Abacus". totton.idirect.com. Archived from the original on 2019-07-06. Retrieved 2019-06-26 .
^ "Base four^2 Hexadecimal Symbol Proposal". Hauptmech. Archived from the original on 2021-x-20. Retrieved 2008-09-04 .
^ "Intuitor Hex Headquarters". Intuitor. Archived from the original on 2010-09-04. Retrieved 2018-x-28 .
^ Niemietz, Ricardo Cancho (2003-10-21). "A proposal for addition of the vi Hexadecimal digits (A-F) to Unicode". DKUUG Standardizing. Archived from the original on 2011-06-04. Retrieved 2018-10-28 .
^ Nystrom, John William (1862). Project of a New System of Arithmetics, Weight, Measure out and Coins: Proposed to be called the Tonal System, with Sixteen to the Base. Philadelphia: Lippincott.
^ Nystrom (1862), p. 33: "In expressing time, angle of a circle, or points on the compass, the unit of measurement tim should exist noted every bit integer, and parts thereof as tonal fractions, as 5·86 tims is five times and metonby [*"sutim and metonby" John Nystrom accidentally gives part of the number in decimal names; in Nystrom's pronunciation scheme, five=su, viii=me, 6=past, c.f. unifoundry.com Archived 2021-05-19 at the Wayback Machine ]."
^ C. East. Fröberg, Hexadecimal Conversion Tables, Lund (1952).
^ The Century Dictionary of 1895 has sexadecimal in the more than full general sense of "relating to 16". An early explicit employ of sexadecimal in the sense of "using base sixteen" is institute also in 1895, in the Journal of the American Geographical Lodge of New York, vols. 27–28, p. 197.
^ Schwartzman, S. (1994). The Words of Mathematics: an etymological dictionary of mathematical terms used in English. ISBN 0-88385-511-ix.
^ Knuth, Donald. (1969). The Art of Computer Programming, Volume 2. ISBN 0-201-03802-1. (Chapter 17.)
^ Alfred B. Taylor, Report on Weights and Measures, Pharmaceutical Association, 8th Annual Session, Boston, fifteen September 1859. Encounter pages and 33 and 41.
^ Alfred B. Taylor, "Octonary numeration and its application to a system of weights and measures", Proc Amer. Phil. Soc. Vol XXIV Archived 2016-06-24 at the Wayback Machine, Philadelphia, 1887; pages 296–366. See pages 317 and 322.
^ IBM System/360 FORTRAN IV Language Archived 2021-05-19 at the Wayback Auto (1966), p. 13.

hoseytheitheave1946.blogspot.com

Source: https://en.wikipedia.org/wiki/Hexadecimal